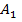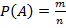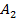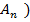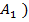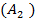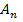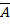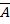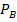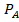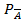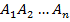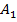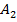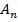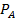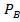Tigr,
Исходя из изложенного г-ном Сивковым посчитать вероятность указанного события решительно невозможно.
совершенно согласен , но изложение исходных данных для расчета вероятности события выходит за рамки статьи.
вы сможете сделать запрашиваемое мною
нет конечно немного теории
Классическое определение вероятности.
Вероятностью события A называется отношение числа исходов m, благоприятствующих наступлению данного события
к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.
– вероятность случайного события
Вероятность любого события не может быть меньше нуля и больше единицы, т.е. 0≤P(A)≤1
Невозможному событию соответствует вероятность P(A)=0, а достоверному – вероятность P(A)=1
Теоремы сложения вероятностей.
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B);
P(
+
+…+
=P(
+P
+…+P(
).
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B)=P(A)+P(B)-P(AB)
Для трех совместных событий имеет место формула:
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
Событие, противоположное событию A (т.е. ненаступление события A), обозначают
. Сумма вероятностей двух противоположных событий равна единице: P(A)+P(
)=1
Вероятность наступления события A, вычисленная в предположении, что событие B уже произошло, называется
условной вероятностью события A при условии B и обозначается
(A) или P(A/B).
Если A и B – независимые события, то
P(B)-
(B)=
(B).
События A,B,C,… называются
независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.
Теоремы умножения вероятностей.
Теорема умножения вероятностей независимых событий.
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
P(AB)=P(A)•P(B)
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле:
P(
)=P(
)•P(
)… P(
).
Теорема умножения вероятностей зависимых событий.
Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
P(AB)=P(A)•
(B)=P(B)•
(A)
при расчете скажем вероятности поражения учитывается много факторов и там довольно сложные формулы , то что я привел это что то типа таблицы умножения , по вероятности события.